ECEF Coordinate System
An in depth explanation of the ECEF coordinate system and how it’s used in the WRLD maps to render the globe accurately. This section also illustrates examples on how to convert from the familiar Mercator projection (Latitude-Longitude) to the more accurate ECEF system.
ECEF
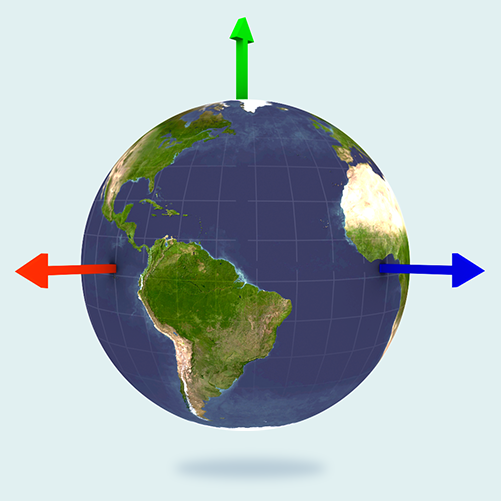
Our ECEF coordinate system is a subtle variation of the Earth Centred Earth Fixed system that we find more appropriate. This coordinate system has a few postulates listed below:
- The origin (0,0,0) is the centre of mass of the earth.
- The positive X axis passes through the Americas at LatLong(0, -90)
- The positive Y axis passes through the South-North pole
- The positive Z axis passes through the prime meridian (0 longitude) at LatLong(0, 0)
For simplicity, we consider the Earth a perfect sphere of radius 6,378,100m. Therefore the exact ECEF position of the north pole would be (0, 6378100.0, 0).
Note: All units are in metres.
Visualised, the axes of our ECEF space would look like:
ECEF and Lat-Long Conversions
Lat-Long to ECEF
To convert from Latitude-Longitude pairs (which are usually in degrees) to ECEF metres:
using Wrld.Space;
{
double latitude = 50.0;
double longitude = 4.0;
var ll = LatLong.FromDegrees(latitude, longitude);
var ecefPosition = ll.ToECEF();
}In the above example the altitude is by default taken to be 0.
Altitude in the LatLongAltitude type is measured in metres above the surface of the perfect sphere (which is considered sea level).
While this is an approximation the standard error remains rather low.
using Wrld.Space;
{
double latitude = 50.0;
double longitude = 4.0;
double heightAboveSeaLevelMeters = 100.0;
var ll = LatLongAltitude.FromDegrees(latitude, longitude, heightAboveSeaLevelMeters);
var ecefPosition = ll.ToECEF();
}Both types LatLong and LatLongAltitude are interchangeable although LatLongAltitude is the base/common type between the two.
ECEF to Lat-Long
You can quickly convert between an ECEF Vector3D and a LatLongAltitude as such:
using Wrld.Space;
using Wrld.Common.Maths;
{
var ecefNorthPole = new DoubleVector3(0.0, 6378100.0, 0.0);
var lla = LatLongAltitude.FromECEF(ecefNorthPole);
}Positioning Objects on the Surface
ECEF Tangent Coordinate Frame
Apps often need to position and orient objects in a coordinate frame that is tangential to the Earth’s surface. For some point on the Earth’s surface, the patch of the Earth sphere that is locally around that point is approximately flat. We can use this tangent plane to define a local coordinate system that is useful for positioning objects relative to this reference frame.
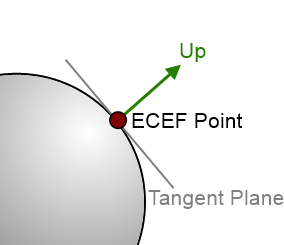
The up direction is perpendicular to the tangent plane – so is in the same direction as a ray from the Earth’s centre passing through our ECEF point on the sphere surface.
The forward and right directions lie on the tangent plane, perpendicular to each other.
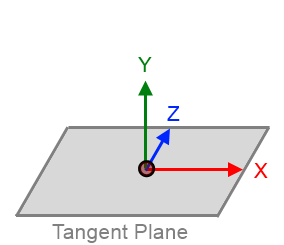
Conventionally, we use a left-handed coordinate system, where:
- The positive X axis points right
- The positive Y axis points up
- The positive Z axis points forward
We provide a class to assist in defining such a coordinate frame: EcefTangentBasis. This can be constructed from an ECEF point and a forward “heading” direction. The class uses these to create the 3 orthogonal basis direction vectors, constrained as described above.